Hier, j'ai découvert que The Golden Ratio: The Story of Phi, the World’s Most Astonishing Number, livre souvent cité
de Mario Livio sur le nombre d'or, était lisible en ligne gratis. Comme je pense que l'accessibilité du site résulte d'une erreur, je ne donne pas son adresse qu'on découvrira aisément si l'erreur perdure, en tout cas le radin que je suis en a profité pour lire l'opus.
Livio est astrophysicien à la NASA, quelqu'un d'a priori sérieux donc. Il reprend la plupart des allégations autour du nombre d'or, en les démystifiant le plus souvent sainement, insistant néanmoins sur les réelles propriétés de Phi et son intervention à de multiples niveaux dans la nature.
Livio donne souvent Phi avec 10 décimales, notamment pages 80-81 où il expose les propriétés fondamentales:
Phi ....= 1.6180339887...
1/Phi = 0.6180339887...
Phi² ..= 2.6180339887...
Or je me rappelle que mes études bachiennes m'ont amené au nombre 887, se partageant idéalement selon le nombre d'or en 339 et 548.
Ainsi on pourrait écrire l'approximation
339 x 2.618 = 887
En fait 339 x Phi² donne 887.51... qu'il faudrait arrondir à 888, mais les décimales suivantes de Phi² sont 2.618033988749... qui, arrondi à 11 décimales, donne
2.618 0339 8875 permettant la permutation
3390 x 2.618 = 8875 (8875.02 exactement)
J'ai déjà rencontré une curiosité avec Phi² arrondi à 2.618, détaillée ici.
En bref un poème basé sur les nombres de Fibonacci avait ses strophes successives en rapport Phi², avec une pénultième strophe de 273 lettres et une dernière de 714 lettres, or:
273 x 2.618 = 714.714 (exactement)
Je suis ensuite arrivé page 85 à une figure immédiatement évocatrice:
de Mario Livio sur le nombre d'or, était lisible en ligne gratis. Comme je pense que l'accessibilité du site résulte d'une erreur, je ne donne pas son adresse qu'on découvrira aisément si l'erreur perdure, en tout cas le radin que je suis en a profité pour lire l'opus.Livio est astrophysicien à la NASA, quelqu'un d'a priori sérieux donc. Il reprend la plupart des allégations autour du nombre d'or, en les démystifiant le plus souvent sainement, insistant néanmoins sur les réelles propriétés de Phi et son intervention à de multiples niveaux dans la nature.
Livio donne souvent Phi avec 10 décimales, notamment pages 80-81 où il expose les propriétés fondamentales:
Phi ....= 1.6180339887...
1/Phi = 0.6180339887...
Phi² ..= 2.6180339887...
Or je me rappelle que mes études bachiennes m'ont amené au nombre 887, se partageant idéalement selon le nombre d'or en 339 et 548.
Ainsi on pourrait écrire l'approximation
339 x 2.618 = 887
En fait 339 x Phi² donne 887.51... qu'il faudrait arrondir à 888, mais les décimales suivantes de Phi² sont 2.618033988749... qui, arrondi à 11 décimales, donne
2.618 0339 8875 permettant la permutation
3390 x 2.618 = 8875 (8875.02 exactement)
J'ai déjà rencontré une curiosité avec Phi² arrondi à 2.618, détaillée ici.
En bref un poème basé sur les nombres de Fibonacci avait ses strophes successives en rapport Phi², avec une pénultième strophe de 273 lettres et une dernière de 714 lettres, or:
273 x 2.618 = 714.714 (exactement)
Je suis ensuite arrivé page 85 à une figure immédiatement évocatrice:
Je rappelle le patch-quilt d'avril dernier, réalisé par ma compagne Anne 
sur une idée à moi. L'assemblage des pièces effectué, j'ai découvert la propriété de deux diagonales, et j'ai demandé à Anne de la magnifier par un quiltage approprié.
Ainsi cette propriété était connue, ce qui n'est pas étonnant en soi. Il l'est un peu plus qu'elle soit illustrée par un rectangle d'or où ont été construits successivement 6 carrés en reportant la largeur sur la longueur (le rectangle restant étant doré), or le patch-quilt est constitué de 6 blocs carrés ajoutés à un rectangle d'or de départ. Ainsi, en tournant le patch de 180°, et en ajustant l'échelle, ses lignes de quiltage coïncideraient exactement avec la figure 26.
J'apprends encore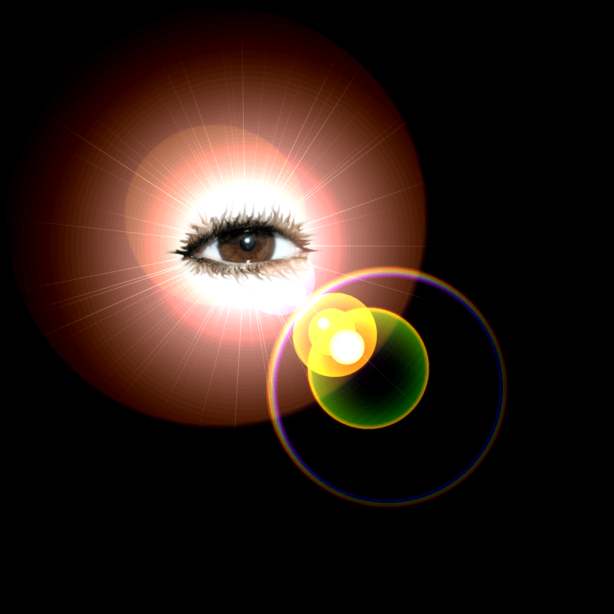
que l'intersection de ces deux diagonales a été baptisée Oeil de Dieu par le mathématicien Cliff Pickover, qui a un magnifique site dont j'extrais la composition en carré ci-contre (où la pupille de l'oeil est à une intersection d'or).
Ce n'est pas banal de trouver cet Oeil de Dieu sur la figure 26 du livre de Mario Livio (qui, d'origine juive, est également citoyen israélien), car 26 est la valeur numérique du fameux Tétragramme, le nom essentiel de Dieu en hébreu, YHVH.
Il s'agit en fait en VO d'un Eye of God, et les numérologues anglo-saxons ont constaté que la valeur numérique de GOD était aussi 26 (7+15+4).
sur une idée à moi. L'assemblage des pièces effectué, j'ai découvert la propriété de deux diagonales, et j'ai demandé à Anne de la magnifier par un quiltage approprié.Ainsi cette propriété était connue, ce qui n'est pas étonnant en soi. Il l'est un peu plus qu'elle soit illustrée par un rectangle d'or où ont été construits successivement 6 carrés en reportant la largeur sur la longueur (le rectangle restant étant doré), or le patch-quilt est constitué de 6 blocs carrés ajoutés à un rectangle d'or de départ. Ainsi, en tournant le patch de 180°, et en ajustant l'échelle, ses lignes de quiltage coïncideraient exactement avec la figure 26.
J'apprends encore
que l'intersection de ces deux diagonales a été baptisée Oeil de Dieu par le mathématicien Cliff Pickover, qui a un magnifique site dont j'extrais la composition en carré ci-contre (où la pupille de l'oeil est à une intersection d'or).Ce n'est pas banal de trouver cet Oeil de Dieu sur la figure 26 du livre de Mario Livio (qui, d'origine juive, est également citoyen israélien), car 26 est la valeur numérique du fameux Tétragramme, le nom essentiel de Dieu en hébreu, YHVH.
Il s'agit en fait en VO d'un Eye of God, et les numérologues anglo-saxons ont constaté que la valeur numérique de GOD était aussi 26 (7+15+4).
Livio consacre plusieurs chapitres à l'art, avec pour optique de démontrer que le caractère esthétique de la section d'or est largement surestimé, et que les spéculations la montrant en oeuvre dans les créations antiques sont fumeuses.
Si je suis plutôt d'accord, je déplore que l'auteur se soit borné à réfuter les allégations touchant les créations les plus célèbres, comme Kheops, le Parthénon, les peintures de Léonard de Vinci, alors qu'il existe des cas bien plus troublants (Notre-Dame du Port par exemple).
Pour la peinture plus récente (19e), Livio semble reprendre l'argumentation de Marguerite Neveux, bien que je n'aie pas vu son nom mentionné. Il n'est encore une fois question que d'oeuvres archi-connues, et donc pas de mon aïeul et des étranges formats dorés récurrents dans ses oeuvres.
Livio ne se limite pas à la France, et je ne suis plus vraiment d'accord quand il exclut Mondrian des peintres pouvant avoir employé la section dorée, malgré l'avis "autorisé" du plus grand spécialiste de Mondrian qui lui a affirmé que, selon lui, le peintre n'avait jamais eu recours à aucune échelle de proportion.
Une reproduction de Broadway Boogie-woogie (1942) est donnée, un tableau carré où certains ont vu une composition dorée, ce à quoi il est facile de rétorquer comme Livio qu'il y a tant de lignes diversement espacées qu'on peut y imaginer n'importe quoi. Je
m'étonne qu'il ne soit pas fait plutôt référence à Composition with Gray and light Brown (1918), ci-contre, le tableau le plus cité par les zélateurs de la section d'or.
Je ne suis absolument
pas spécialiste de Mondrian, mais cette oeuvre me semble suffisante à elle seule pour justifier les revendications dorées.
D'abord le format donné (802 x 498 mm après conversion) est pratiquement idéalement doré (802 x 496 idéal). J'ai tracé aussi rigoureusement que possible les 4 sections d'or, on voit qu'elles se superposent assez bien à 4 lignes du tableau, délimitant un net rectangle central, et c'est le SEUL rectangle symétrique par rapport au centre de l'oeuvre.
En fait l'approche dorée parfaite n'est peut-être pas la meilleure, car le format donné est aussi proche de 1.6 (80 x 50 cm), et l'examen de détail révèle que la hauteur comme la largeur sont divisées en 16 bandes par 15 lignes épaisses qui, bien que peintes grossièrement, ce qui donne une dynamique à l'oeuvre, sont appliquées sur une grille de 16x16 cases préalablement tracée sur la toile. L'interruption des lignes fait qu'il n'y a pas 256 unités rectangulaires mais 67, parmi lesquels 18 sont des rectangles de format proportionnel à celui de la toile, sans compter les rectangles formés par association, comme le rectangle central qui correspond à 16 unités, soit 1/16e de la surface totale au format 1.6...
Je n'analyse pas plus loin. On retombe ici dans la facile confusion entre section à 5/8es, connue des peintres du 19e, et section d'or idéale, mais je crois avoir montré qu'au moins ce tableau témoigne d'une certaine intention numérologique, quelle qu'elle soit.
Si je suis plutôt d'accord, je déplore que l'auteur se soit borné à réfuter les allégations touchant les créations les plus célèbres, comme Kheops, le Parthénon, les peintures de Léonard de Vinci, alors qu'il existe des cas bien plus troublants (Notre-Dame du Port par exemple).
Pour la peinture plus récente (19e), Livio semble reprendre l'argumentation de Marguerite Neveux, bien que je n'aie pas vu son nom mentionné. Il n'est encore une fois question que d'oeuvres archi-connues, et donc pas de mon aïeul et des étranges formats dorés récurrents dans ses oeuvres.
Livio ne se limite pas à la France, et je ne suis plus vraiment d'accord quand il exclut Mondrian des peintres pouvant avoir employé la section dorée, malgré l'avis "autorisé" du plus grand spécialiste de Mondrian qui lui a affirmé que, selon lui, le peintre n'avait jamais eu recours à aucune échelle de proportion.
Une reproduction de Broadway Boogie-woogie (1942) est donnée, un tableau carré où certains ont vu une composition dorée, ce à quoi il est facile de rétorquer comme Livio qu'il y a tant de lignes diversement espacées qu'on peut y imaginer n'importe quoi. Je
m'étonne qu'il ne soit pas fait plutôt référence à Composition with Gray and light Brown (1918), ci-contre, le tableau le plus cité par les zélateurs de la section d'or.Je ne suis absolument
pas spécialiste de Mondrian, mais cette oeuvre me semble suffisante à elle seule pour justifier les revendications dorées.D'abord le format donné (802 x 498 mm après conversion) est pratiquement idéalement doré (802 x 496 idéal). J'ai tracé aussi rigoureusement que possible les 4 sections d'or, on voit qu'elles se superposent assez bien à 4 lignes du tableau, délimitant un net rectangle central, et c'est le SEUL rectangle symétrique par rapport au centre de l'oeuvre.
En fait l'approche dorée parfaite n'est peut-être pas la meilleure, car le format donné est aussi proche de 1.6 (80 x 50 cm), et l'examen de détail révèle que la hauteur comme la largeur sont divisées en 16 bandes par 15 lignes épaisses qui, bien que peintes grossièrement, ce qui donne une dynamique à l'oeuvre, sont appliquées sur une grille de 16x16 cases préalablement tracée sur la toile. L'interruption des lignes fait qu'il n'y a pas 256 unités rectangulaires mais 67, parmi lesquels 18 sont des rectangles de format proportionnel à celui de la toile, sans compter les rectangles formés par association, comme le rectangle central qui correspond à 16 unités, soit 1/16e de la surface totale au format 1.6...
Je n'analyse pas plus loin. On retombe ici dans la facile confusion entre section à 5/8es, connue des peintres du 19e, et section d'or idéale, mais je crois avoir montré qu'au moins ce tableau témoigne d'une certaine intention numérologique, quelle qu'elle soit.
Je n'ai développé ici que les quelques points qui m'ont fait particulièrement réagir. Le livre de Livio me semble globalement satisfaisant, par rapport à ce que nous avons en France, malgré de nombreuses imprécisions et un certain sensationnalisme présent dès le titre, ce qui est probablement un impératif éditorial.
Le mathématicien George Markowski donne ici une critique plus sévère, estimant que Livio lui a emprunté beaucoup de choses sans souvent préciser sa source. Mais
Markowski se trompe en dénigrant l'analyse par Livio de La dernière Cène de Dali, avançant que Dali a écrit sur son oeuvre et n'a jamais mentionné son utilisation du nombre d'or. Or il est bien connu que ce tableau et d'autres de cette période doivent beaucoup à la rencontre entre Dali et Matila Ghyka. Il existe ainsi une lettre de Ghyka à Dali datée du 13 août 1947 (le 8/13 !) où Ghyka se déclare ravi d'apprendre que Dali a utilisé ses recommandations pour la composition de Leda atomica, ci-contre, en réponse évidente à un courrier antérieur.
Je me rappelle d'un documentaire montrant Dali clamer qu'il méprisait tout peintre qui serait incapable de situer d'emblée la section d'or d'un tableau. Pour la Leda, la ligne d'horizon correspond à la section d'or supérieure, sans préjuger d'autres harmonies calculées.
Le mathématicien George Markowski donne ici une critique plus sévère, estimant que Livio lui a emprunté beaucoup de choses sans souvent préciser sa source. Mais
Markowski se trompe en dénigrant l'analyse par Livio de La dernière Cène de Dali, avançant que Dali a écrit sur son oeuvre et n'a jamais mentionné son utilisation du nombre d'or. Or il est bien connu que ce tableau et d'autres de cette période doivent beaucoup à la rencontre entre Dali et Matila Ghyka. Il existe ainsi une lettre de Ghyka à Dali datée du 13 août 1947 (le 8/13 !) où Ghyka se déclare ravi d'apprendre que Dali a utilisé ses recommandations pour la composition de Leda atomica, ci-contre, en réponse évidente à un courrier antérieur.Je me rappelle d'un documentaire montrant Dali clamer qu'il méprisait tout peintre qui serait incapable de situer d'emblée la section d'or d'un tableau. Pour la Leda, la ligne d'horizon correspond à la section d'or supérieure, sans préjuger d'autres harmonies calculées.
Aucun commentaire:
Enregistrer un commentaire